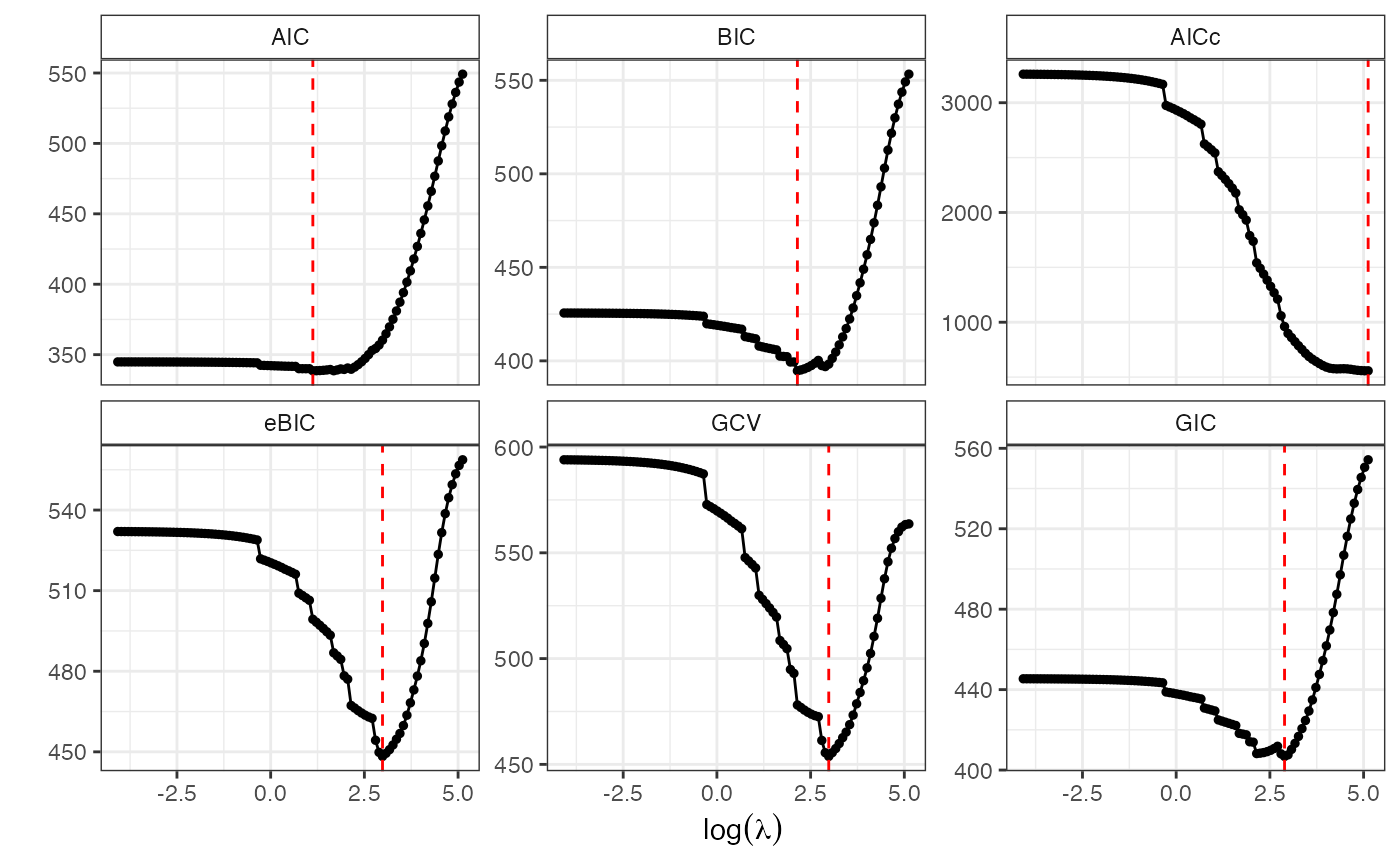
Select Optimal Lambda via Goodness-of-Fit Criteria

Extracts the tuning parameter lambda minimizing multiple information criteria from a fitted islasso.path object. Supported criteria include AIC, BIC, AICc, eBIC, GCV, and GIC.

Usage

GoF.islasso.path(object, plot = TRUE, ...)

Arguments

object: A fitted model of class "islasso.path".
plot: Logical. If TRUE (default), displays plots for each criterion over the lambda path.
...: Additional arguments passed to lower-level plotting or diagnostic methods.

Value

A list with components:

gof: Matrix of goodness-of-fit values across lambda values.
minimum: Index positions of the minimum for each criterion.
lambda.min: Optimal lambda values that minimize each criterion.

Details

This function identifies the optimal regularization parameter lambda by minimizing various information-based selection criteria. Degrees of freedom are computed as the trace of the hat matrix, which may be fractional under induced smoothing. This provides a robust alternative to cross-validation, especially in high-dimensional settings.

Author

Gianluca Sottile gianluca.sottile@unipa.it

Examples

set.seed(1)
n <- 100; p <- 30
beta <- c(runif(10, -2, 2), rep(0, p - 10))
sim <- simulXy(n = n, p = p, beta = beta, seed = 1, family = gaussian())
fit <- islasso.path(y ~ ., data = sim$data, family = gaussian())
GoF.islasso.path(fit)

#> $gof
#>             AIC      BIC      AICc     eBIC      GCV      GIC
#>   [1,] 344.8518 425.5860 3260.2150 532.0052 593.9714 445.3931
#>   [2,] 344.8500 425.5817 3259.9984 531.9977 593.9552 445.3882
#>   [3,] 344.8479 425.5769 3259.7597 531.9894 593.9374 445.3828
#>   [4,] 344.8456 425.5716 3259.4928 531.9801 593.9175 445.3767
#>   [5,] 344.8431 425.5657 3259.1978 531.9698 593.8955 445.3700
#>   [6,] 344.8403 425.5593 3258.8742 531.9585 593.8713 445.3627
#>   [7,] 344.8372 425.5522 3258.5191 531.9461 593.8449 445.3546
#>   [8,] 344.8339 425.5445 3258.1294 531.9326 593.8158 445.3458
#>   [9,] 344.8303 425.5360 3257.7018 531.9177 593.7839 445.3361
#>  [10,] 344.8262 425.5266 3257.2305 531.9013 593.7488 445.3254
#>  [11,] 344.8219 425.5164 3256.7162 531.8834 593.7105 445.3138
#>  [12,] 344.8170 425.5052 3256.1514 531.8637 593.6685 445.3010
#>  [13,] 344.8118 425.4929 3255.5313 531.8422 593.6224 445.2870
#>  [14,] 344.8060 425.4794 3254.8478 531.8184 593.5715 445.2715
#>  [15,] 344.7997 425.4646 3254.1018 531.7925 593.5161 445.2547
#>  [16,] 344.7928 425.4484 3253.2825 531.7641 593.4552 445.2362
#>  [17,] 344.7852 425.4306 3252.3790 531.7327 593.3882 445.2159
#>  [18,] 344.7770 425.4111 3251.3929 531.6985 593.3151 445.1937
#>  [19,] 344.7679 425.3897 3250.3052 531.6608 593.2345 445.1692
#>  [20,] 344.7580 425.3664 3249.1176 531.6197 593.1466 445.1426
#>  [21,] 344.7472 425.3407 3247.8073 531.5744 593.0497 445.1132
#>  [22,] 344.7354 425.3126 3246.3768 531.5249 592.9440 445.0812
#>  [23,] 344.7225 425.2818 3244.7982 531.4704 592.8276 445.0459
#>  [24,] 344.7084 425.2480 3243.0676 531.4107 592.7001 445.0074
#>  [25,] 344.6932 425.2112 3241.1769 531.3455 592.5610 444.9653
#>  [26,] 344.6764 425.1707 3239.0896 531.2737 592.4077 444.9190
#>  [27,] 344.6582 425.1264 3236.8007 531.1950 592.2399 444.8683
#>  [28,] 344.6384 425.0780 3234.2894 531.1089 592.0562 444.8128
#>  [29,] 344.6169 425.0250 3231.5332 531.0145 591.8549 444.7521
#>  [30,] 344.5935 424.9671 3228.5078 530.9110 591.6346 444.6857
#>  [31,] 344.5682 424.9038 3225.1866 530.7977 591.3933 444.6131
#>  [32,] 344.5407 424.8346 3221.5404 530.6736 591.1291 444.5337
#>  [33,] 344.5108 424.7588 3217.5204 530.5370 590.8388 444.4466
#>  [34,] 344.4788 424.6764 3213.1330 530.3884 590.5230 444.3519
#>  [35,] 344.4441 424.5861 3208.2906 530.2248 590.1757 444.2480
#>  [36,] 344.4068 424.4878 3202.9812 530.0460 589.7964 444.1346
#>  [37,] 344.3667 424.3807 3197.1548 529.8505 589.3821 444.0111
#>  [38,] 344.3238 424.2641 3190.7587 529.6367 588.9294 443.8764
#>  [39,] 344.2781 424.1372 3183.7359 529.4029 588.4349 443.7296
#>  [40,] 344.2293 423.9991 3176.0246 529.1472 587.8949 443.5696
#>  [41,] 344.1768 423.8480 3167.5202 528.8661 587.3021 443.3943
#>  [42,] 342.4509 419.8368 2974.8888 521.8426 572.7934 438.8225
#>  [43,] 342.3552 419.5734 2961.1482 521.3581 571.8125 438.5179
#>  [44,] 342.2654 419.3150 2947.3850 520.8773 570.8417 438.2181
#>  [45,] 342.1657 419.0231 2931.7616 520.3320 569.7437 437.8790
#>  [46,] 342.0760 418.7417 2916.2622 519.7981 568.6718 437.5506
#>  [47,] 341.9899 418.4540 2900.0324 519.2446 567.5643 437.2135
#>  [48,] 341.9028 418.1464 2882.3658 518.6463 566.3710 436.8517
#>  [49,] 341.8074 417.7985 2862.2442 517.9656 565.0182 436.4419
#>  [50,] 341.7543 417.5234 2844.6765 517.3979 563.8946 436.1124
#>  [51,] 341.7070 417.2341 2825.6360 516.7897 562.6950 435.7637
#>  [52,] 341.6638 416.9229 2804.6713 516.1253 561.3897 435.3868
#>  [53,] 340.0503 412.9502 2624.0547 509.0427 547.7409 430.8353
#>  [54,] 340.0137 412.5674 2598.5204 508.2035 546.1651 430.3675
#>  [55,] 339.9996 412.1796 2571.2088 507.3232 544.5221 429.8880
#>  [56,] 340.0119 411.7972 2542.6290 506.4206 542.8478 429.4088
#>  [57,] 338.5380 407.9071 2371.4958 499.3456 529.9186 424.9260
#>  [58,] 338.5976 407.4700 2337.7943 498.2536 527.9897 424.3669
#>  [59,] 338.7092 407.0403 2301.5595 497.1105 525.9887 423.8045
#>  [60,] 338.8837 406.6313 2263.0423 495.9324 523.9461 423.2524
#>  [61,] 339.1278 406.2397 2221.7144 494.7029 521.8358 422.7048
#>  [62,] 339.4479 405.8687 2177.5184 493.4209 519.6588 422.1642
#>  [63,] 338.5773 402.5444 2024.2216 486.8622 508.5448 418.2379
#>  [64,] 339.1569 402.3694 1979.6532 485.6926 506.6829 417.8778
#>  [65,] 339.8634 402.2255 1930.4316 484.4277 504.6928 417.5252
#>  [66,] 339.5143 399.3822 1789.3538 478.2967 494.8630 414.0700
#>  [67,] 340.5223 399.4146 1737.5826 477.0432 493.0190 413.8631
#>  [68,] 339.6438 394.6916 1540.6641 467.2525 478.0742 408.1969
#>  [69,] 341.1542 395.1469 1491.6152 466.3171 476.8943 408.3933
#>  [70,] 342.9131 395.7245 1438.3696 465.3376 475.6789 408.6811
#>  [71,] 344.9600 396.5071 1383.3962 464.4536 474.6302 409.1535
#>  [72,] 347.3140 397.5048 1326.6648 463.6635 473.7376 409.8185
#>  [73,] 349.9967 398.7450 1268.8295 463.0022 473.0414 410.7048
#>  [74,] 353.0119 400.2369 1210.4856 462.4862 472.5517 411.8230
#>  [75,] 354.3793 397.4867 1058.6479 454.3084 461.3238 408.0625
#>  [76,] 356.8227 396.9392  960.9334 449.8185 455.5101 406.7813
#>  [77,] 360.3045 398.2637  897.7395 448.2993 453.7622 407.5765
#>  [78,] 364.7950 401.3166  860.3133 449.4573 455.5236 410.2767
#>  [79,] 369.7306 404.7077  822.4028 450.8126 457.4733 413.2889
#>  [80,] 375.1416 408.5393  786.2950 452.5622 459.8474 416.7330
#>  [81,] 381.0222 412.8062  752.1034 454.7020 462.6173 420.6040
#>  [82,] 387.2646 417.2803  717.1030 456.8453 465.2548 424.6443
#>  [83,] 394.0636 422.4138  687.5502 459.7835 468.7744 429.3692
#>  [84,] 401.4904 428.2976  663.4081 463.6332 473.3049 434.8743
#>  [85,] 409.5076 434.8453  643.2134 468.2439 478.6307 441.0615
#>  [86,] 417.9681 441.7280  623.3543 473.0470 483.9832 447.5572
#>  [87,] 426.8405 448.9992  605.5309 478.2076 489.5697 454.4356
#>  [88,] 436.0899 456.7146  591.0983 483.9010 495.6256 461.7746
#>  [89,] 445.6813 464.9395  581.1248 490.3245 502.4339 469.6642
#>  [90,] 455.6308 473.8274  576.8541 497.8130 510.4830 478.2917
#>  [91,] 465.9895 483.1907  574.6475 505.8643 519.0660 487.4108
#>  [92,] 476.6809 493.0720  575.6531 514.6777 528.5102 497.0933
#>  [93,] 487.5438 503.0492  576.4780 523.4877 537.7465 506.8533
#>  [94,] 498.3487 512.6903  574.9529 531.5945 545.7749 516.2088
#>  [95,] 508.8468 521.7118  571.1986 538.6697 552.1576 524.8680
#>  [96,] 518.8586 529.9566  566.1610 544.5852 556.7642 532.6793
#>  [97,] 527.9878 537.2451  561.8927 549.4477 559.9704 539.5163
#>  [98,] 536.2179 543.6657  559.1670 553.4829 562.1846 545.4929
#>  [99,] 543.5435 549.1808  557.6835 556.6116 563.3318 550.5639
#> [100,] 549.1749 553.2876  557.5319 558.7086 563.6739 554.2965
#> 
#> $minimum
#>  AIC  BIC AICc eBIC  GCV  GIC 
#>   57   68  100   77   77   76 
#> 
#> $lambda.min
#>        AIC        BIC       AICc       eBIC        GCV        GIC 
#>   3.080924   8.563382 167.562870  19.764636  19.764636  18.010610 
#> 
#> $plot

#>